こんにちは。びらとり義経塾の瀬尾です。
現在、中学1年生の数学では、空間図形の学習を進めています。

左は正12面体、右は正20面体です。
面の形はそれぞれ正五角形と正三角形になっています。
とっても美しい✨ですね!
正多面体、つまり全ての面が同じ形、同じ大きさの図形でできた立体は5種類しかありません。
その特徴を表にまとめると次のようになります。
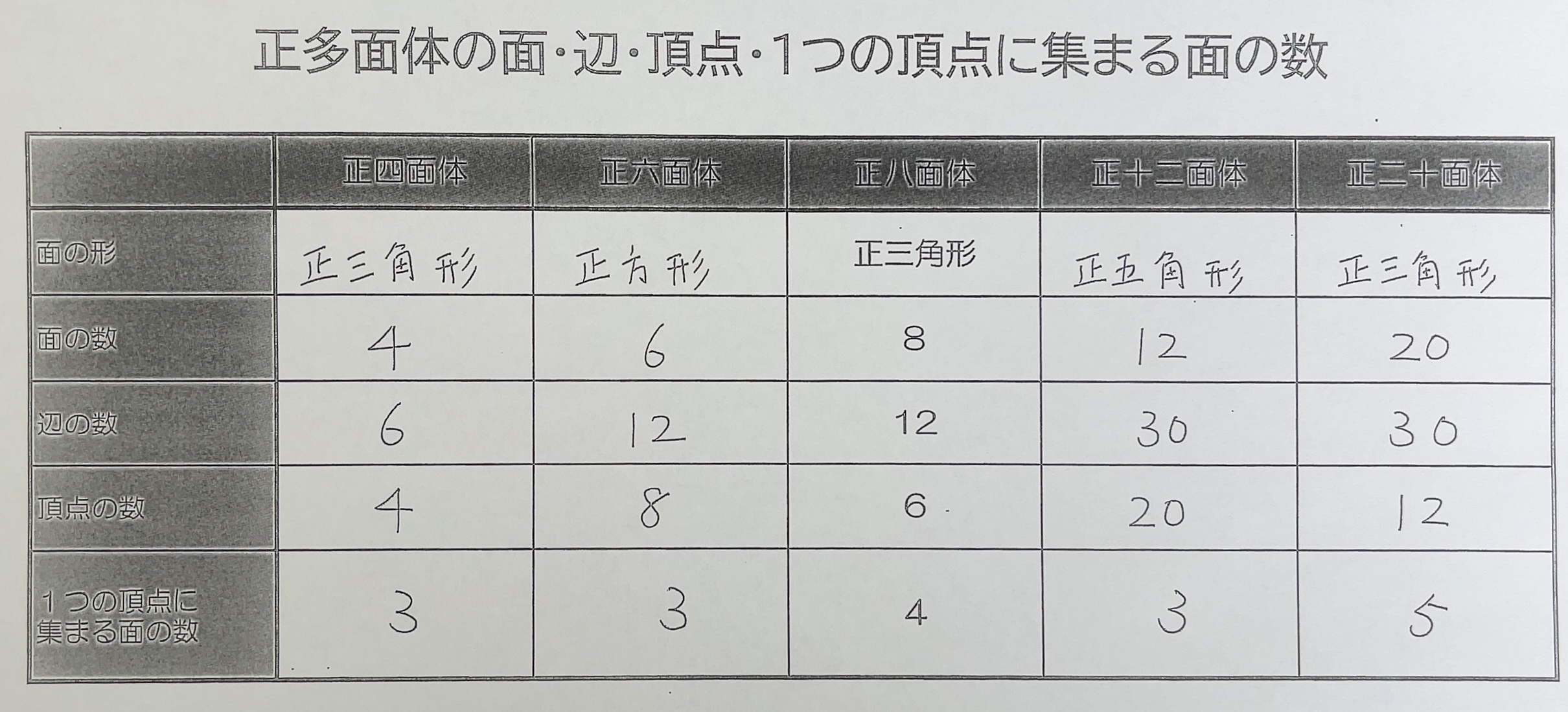
これらの数字、覚えようと思ってもなかなか難しいですよね。
そこで、式から求める方法を正20面体を例にお伝えしたいと思います。
まず、面の数を使います。ここでは、正20面体なので、20です。
次に面の数が分かると、辺の数を次のように計算できます。
(辺の数)=(1つの面の辺の数)×(面の数)÷2
正20面体の面は正三角形なので1つの面の辺の数は3です。
上の公式に当てはめて計算すると、
(辺の数)=3×20÷2=30
となります。
そして、面の数、辺の数が求まれば頂点の数を次のように求めることができます。
(頂点の数)ー(辺の数)+(面の数)=2
数字を当てはめて計算すると
(頂点の数)ー30+20=2
となり、
(頂点の数)=12
と求まります。
これで、面の数、辺の数、頂点の数を計算によって求めることが出来ました。
気になった方は他の正多角形でも試してみてください!
本日のクイズコーナー!
前回の解答:長崎県
今日の問題:望ましい状態で好都合なことを表す慣用句「渡りに○」。
○に入る漢字は何でしょう?
答えは次回のブログで。ではまた✋







